Pengenalan Neural Networks

Tulisan ini adalah catatan belajar PyTorch Udacity Scholar nd188. Semua gambar milik kelas tersebut. Kelas ini sekarang tersedia FREE sebagai ud188.

Neural Networks adalah inti dari Deep Learning, dimana sebetulnya berusaha menirukan bagaimana otak bekerja, dengan syaraf-syaraf yang mengirimkan informasi satu sama lain.

Deep Neural Networks adalah Neural Networks dengan banyak layer.

Membayangkan cara kerja Neural Network yang sederhana adalah membayangkan memisahkan kumpulan dua objek merah dan biru dengan sebuah garis. Dalam hal itu, kumpulan dua objek merah dan biru adalah data yang ada. Neural Networks akan mencari garis dengan posisi terbaik untuk memisahkan kumpulan kedua objek tersebut. Deep Neural Network mampu memisahkan dua kumpulan objek meskipun bentuknya kompleks, tidak semudah seperti garis lurus.

Contoh Kasus Klasifikasi #

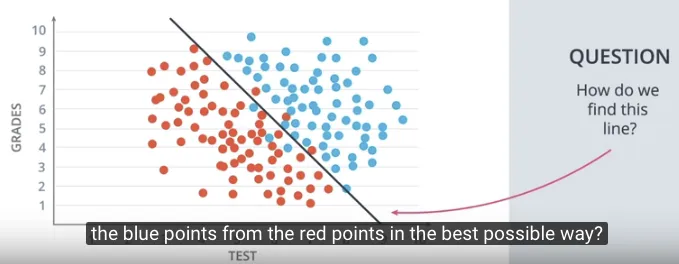
Membuat klasifikasi untuk menentukan apakah seseorang diterima di sebuah kampus berdasarkan 2 informasi, hasil ujiannya dan nilainya di sekolah? dimana dua informasi ini akan digambarkan di koordinat kartesian 2 dimensi.

Kemudian melakukan hal yang dilakukan oleh semua algoritma Machine Learning, yaitu melihat sebaran dari data sebelumnya. Sehingga muncul kumpulan 2 objek, yakni kumpulan yang diterima di kampus dan kumpulan yang ditolak.

Dari kedua kumpulan objek tersebut, dibuat pemisahannya dengan jelas misalnya dengan sebuah garis, sehingga kita dapat melakukan klasifikasi dengan baik. Jka berada di kumpulan objek yang diterima, maka titik (orang) tersebut diterima di kampus. Jika sebuah titik dicek berada di kumpulan objek yang ditolak, maka titik (orang) tersebut akan ditolak di kampus.

Garis yang digunakan dalam pemisahan tersebut adalah model kita dalam menentukan penerimaan di kampus.

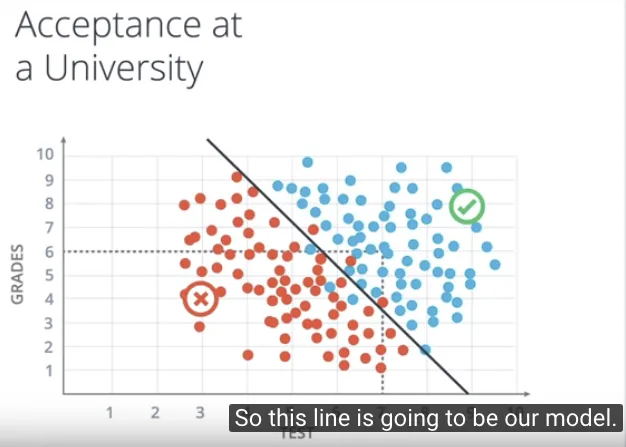
Persamaan Linear (Linear Equation) #

Dalam matematika, persamaan linear (linear equation) untuk garis tersebut digambarkan sebagai persamaan dari 2 informasi:

• test yaitu hasil ujiannya
• grades yaitu nilainya di sekolah

Dengan melakukan prediksi jika suatu nilai dimasukkan dalam persamaan tersebut hasilnya (score) lebih besar atau sama dengan 0 maka akan diterima di kampus, sebaliknya akan ditolak. Berikut adalah gambaran dari model berupa persamaan linear tersebut.

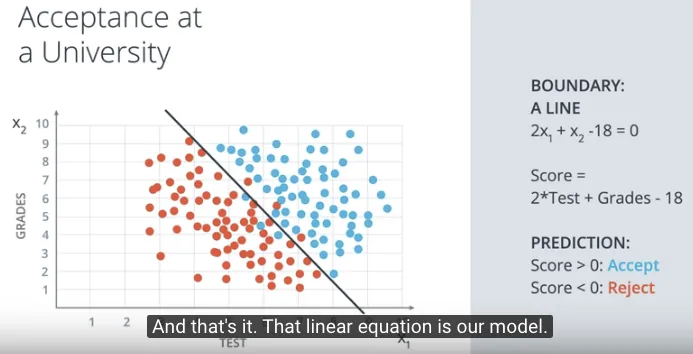
Secara lebih umum, persamaan tersebut dapat dituliskan sebagai berikut:

$w_1x_1 + w_2x_2 + b = 0$

Atau dalam notasi vector dapat dituliskan sebagai:

$Wx + b = 0$

$W = (w_1, w_2)$

$x = (x_1, x_2)$

Dengan referensi x sebagai input, W sebagai weight, dan b sebagai bias.

Untuk titik (orang) $x_1, x_2$ akan diprediksi label sebagai $y$, dituliskan sebagai y = label: 0 or 1. Dimana jika diterima di kampus maka label = 1 dan jika ditolak maka label = 0.

Prediksi tersebut dituliskan sebagai $\hat{y}$ (y hat).

$\hat{y}$ = 1 if $Wx + b >= 0$

$\hat{y}$ = 0 if $Wx + b < 0$

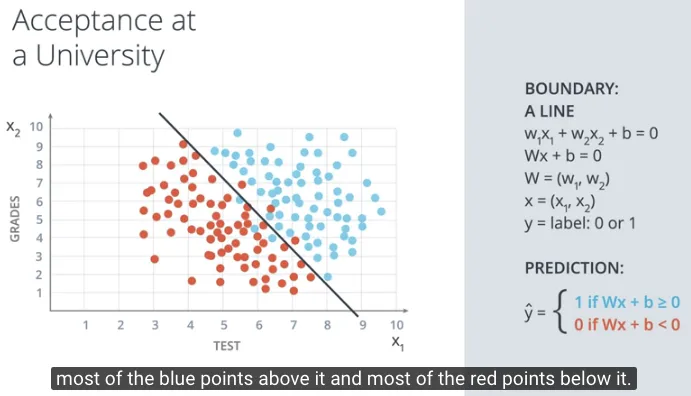
Selanjutnya kita akan mencoba menambahkan satu kolom informasi lagi dengan rank untuk peringkat di kelas, selain dua sebelumnya yaitu test dan grades. Sekarang total menjadi 3 informasi, sehingga digambarkan sebagai koordinat 3-dimensi.

Jika sebelumnya, saat digambarkan dalam koordinat 2 dimensi, pemisah antar kedua objek adalah 1 dimensi, yaitu sebuah garis, maka dalam koordinat 3 dimensi, pemisah antar kedua objek adalah 2 dimensi, yaitu sebuah bidang. Gambarnya sebagai berikut.

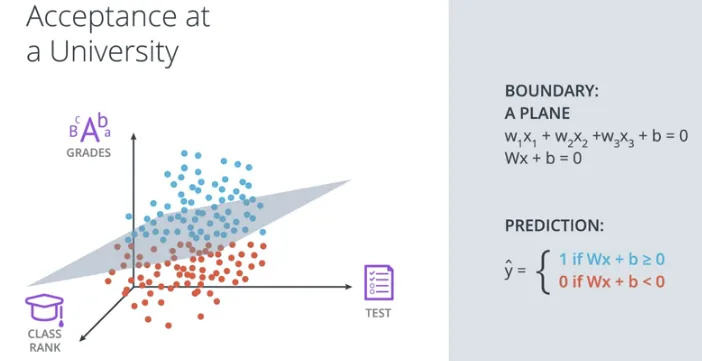
Melihat hal tersebut, jadi sebetulnya jika digambarkan dalam n dimensi maka pemisah antar kedua objek adalah (n-1) dimensi. 🤔 (ya, susah digambarkan, dibayangkan saja..)

Perceptron #

Perceptron adalah komponen pembangun (building block) dalam Neural Networks.

Dalam persamaan linear sebelumnya, dalam contoh kasus klasifikasi penentuan masuk (seleksi) kampus.

$2x_1 + x_2 - 18 = 0$

Artinya suatu score ditentukan dengan 2 * Test + Grades - 18.

Dengan prediksi jika score >= 0 maka diterima masuk kampus dan score < 0 akan ditolak.

Sebagai contoh untuk Test = 7 dan Grades = 6 maka score-nya adalah 2, karena lebih besar dari 0 maka diterima di kampus.

Dalam gagasan tentang Perceptron, notasi perceptron dapat digambarkan sebagai berikut.

Secara lengkap, notikasi persamaan linear dalam klasifikasi seleksi kampus di atas, digambarkan sebagai berikut. Dimana angka 2 (dari Test) dan angka 1 (dari Grades) akan menjadi label masing-masing untuk nilai dari $x_1$ dan $x_2$, lihat pada dua panah di sebelah kiri. Sedangkan angka -18 (dari bias) akan menjadi label untuk node yang di tengah.

Gambaran lain dari perceptron yang lebih sering digunakan adalah memisahkan bias sebagai input seperti pada gambar berikut, sehingga node yang di tengah akan memroses perkalian dari semua input.

Sehingga lengkap dengan proses prediksi, akan membandingkan hasil kalkulasinya apakah lebih besar atau sama dengan 0, sehingga mengembalikan 1 artinya diterima masuk kampus.

Dalam kondisi secara umum, maka digambarkan bahwa ada n input, dengan nilai $x_1, x_2, … x_n$ dan setiap nilai itu punya bobot $w_1, w_2, … w_n$ serta satu nilai bias b.

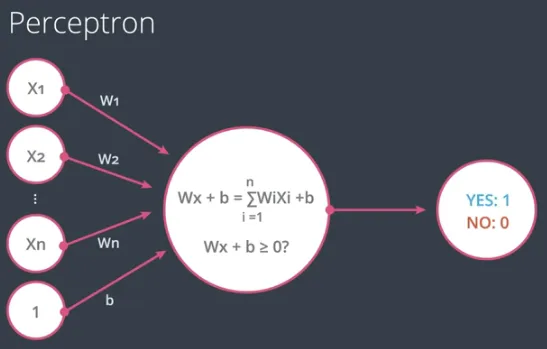
Dalam notasi perceptron tersebut, sebetulnya proses prediksi tersebut secara implisit menggunakan sebuah fungsi yang disebut step function, dimana fungsi tersebut akan menghasilkan 1 jika nilai masukannya sama dengan atau lebih besar dari 0, sebaliknya akan menghasilkan 0 jika nilai masukannya lebih kecil dari 0.

Sehingga dituliskan ulang, notasi perceptron tersebut akan merupakan gabungan dua buah node atau fungsi.

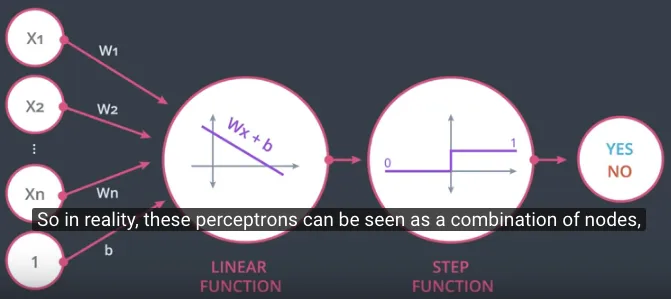
Fungsi yang pertama sebagai linear function (summation ditandai dengan $\sum$) dan fungsi yang kedua adalah step function dimana ke depan akan digunakan beberapa macam step function (ditandai dengan step drawing).

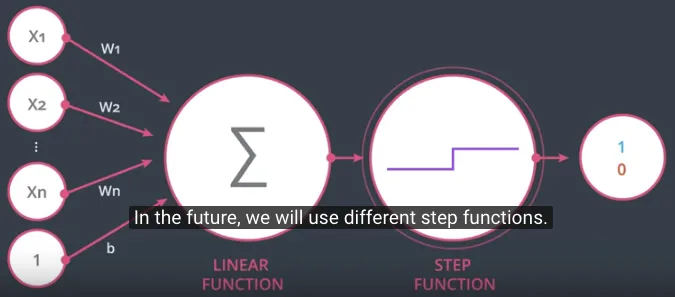
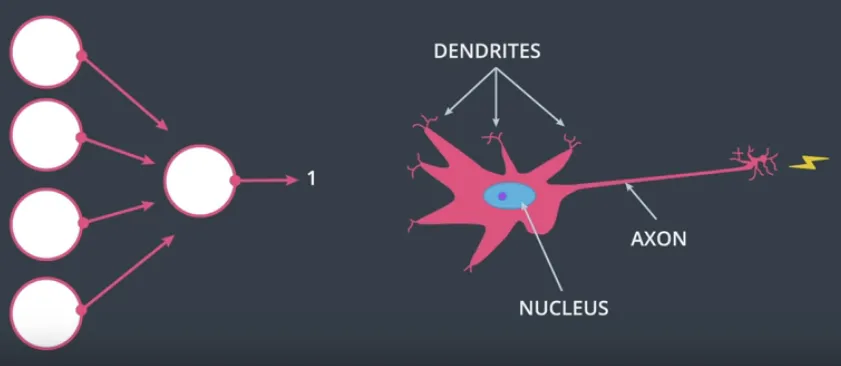
Membandingkan Artificial Neural Networks dengan Biological Neural Networks #

Di gambar ini, sebelah kiri adalah Artificial Neural Networks, atau sering disingkat hanya Neural Networks, yang baru saja dipelajari sebelumnya. Dan di sisi kanan adalah Biological Neural Networks adalah sistem syaraf yang ada di otak manusia, yang ditirukan oleh implementasi Neural Networks.

Menggunakan Perceptron sebagai Operator Logika (AND, OR, NOT) #

Setelah mengetahui gagasan tentang perceptron, kali ini akan dicoba untuk menggunakannya di operasi yang sederhana, yaitu operasi logika (AND, OR, NOT). Atau ada juga yang menyebutkan dengan operasi boolean, karena yang dioperasikan hanya 0 dan 1 (seperti halnya False dan True).

Menggabungkan Sejumlah Operasi pada Perceptron #

Menggunakan perceptron AND, perceptron OR, dan perceptron NOT yang digabungkan menjadi operasi yang sama dengan XOR (exclusive OR).

Perceptron AND #

Operator logika AND, akan menghasilkan 1 (True) jika kedua input bernilai 1, selain itu akan menghasilkan 0 (False).

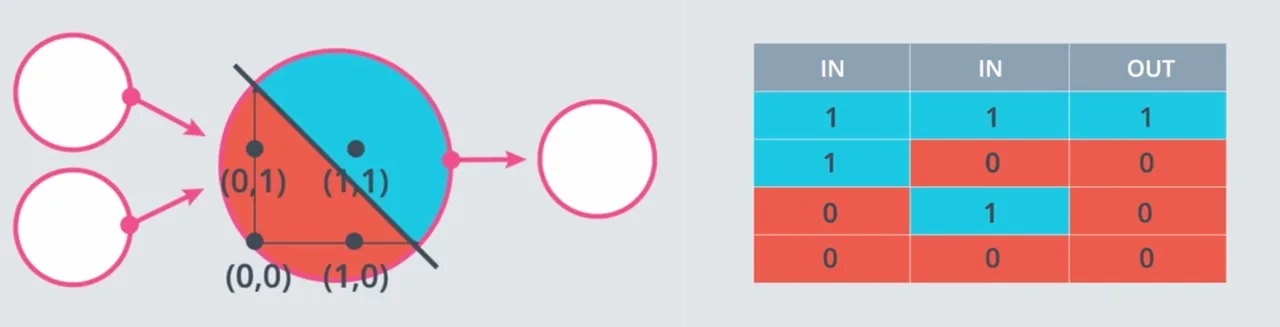
Dengan persamaan linear yang telah dibahas sebelumnya $w_1x_1 + w_2x_2 + b = 0$ kita akan melakukan implementasi dengan program python sederhana untuk mencari berapa nilai weight1, weight2, dan bias untuk implementasi dari perceptron AND.

import pandas as pd

weight1 = 0.0  # TODO
weight2 = 0.0  # TODO
bias = 0.0     # TODO

# DON'T CHANGE ANYTHING BELOW
# Inputs and outputs
test_inputs = [(0, 0), (0, 1), (1, 0), (1, 1)]  # possible input for logic operations
correct_outputs = [False, False, False, True]  # correct output of operator AND
outputs = []

# Generate and check output. iterate for every element of test_inputs and correct_outputs
for test_input, correct_output in zip(test_inputs, correct_outputs):
    # y = w1 x1 + w2 x2 + bias
    linear_combination = weight1 * test_input[0] + weight2 * test_input[1] + bias
    output = int(linear_combination >= 0)
    is_correct_string = 'Yes' if output == correct_output else 'No'
    outputs.append([test_input[0], test_input[1], linear_combination, output, is_correct_string])

# Print output using pandas DataFrame .to_string()
num_wrong = len([output[4] for output in outputs if output[4] == 'No'])
output_frame = pd.DataFrame(outputs, columns=['Input 1', '  Input 2', '  Linear Combination', '  Activation Output', '  Is Correct'])
if not num_wrong:
    print('Nice!  You got it all correct.\n')
else:
    print('You got {} wrong.  Keep trying!\n'.format(num_wrong))
print(output_frame.to_string(index=False))

Perceptron OR #

Operator logika OR, akan menghasilkan 0 (False) jika kedua input bernilai 0, selain itu akan menghasilkan 1 (True).

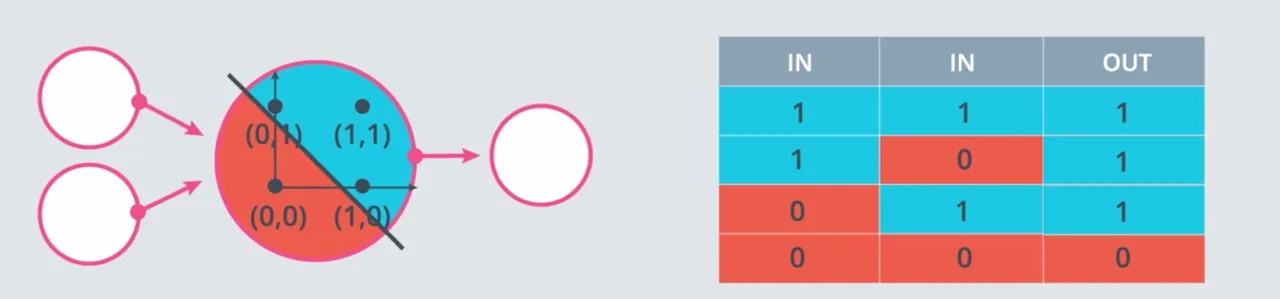
Perceptron NOT #

Operator logina NOT, akan menghasilkan 0 (False) jika satu input bernilai 1, selain itu akan menghasilkan 1 (True) jika satu input bernilai 0.

Perhatikan bahwa perceptron NOT ini hanya beroperasi pada satu masukan, sehingga jika perceptron memiliki dua masukan, pastikan yang mana salah satu dari dua itu yang sebetulnya dioperasikan.

import pandas as pd

weight1 = 0.0  # TODO
weight2 = 0.0  # TODO
bias = 0.0     # TODO


# DON'T CHANGE ANYTHING BELOW
# Inputs and outputs
test_inputs = [(0, 0), (0, 1), (1, 0), (1, 1)]  # possible input for logic operations
# hints: the expected output related to the second value of input (tuple)
correct_outputs = [True, False, True, False]  # correct (expected) output of operator NOT
outputs = []

# Generate and check output. iterate for every element of test_inputs and correct_outputs
for test_input, correct_output in zip(test_inputs, correct_outputs):
    # y = w1 x1 + w2 x2 + bias
    linear_combination = weight1 * test_input[0] + weight2 * test_input[1] + bias
    output = int(linear_combination >= 0)
    is_correct_string = 'Yes' if output == correct_output else 'No'
    outputs.append([test_input[0], test_input[1], linear_combination, output, is_correct_string])

# Print output
num_wrong = len([output[4] for output in outputs if output[4] == 'No'])
output_frame = pd.DataFrame(outputs, columns=['Input 1', '  Input 2', '  Linear Combination', '  Activation Output', '  Is Correct'])
if not num_wrong:
    print('Nice!  You got it all correct.\n')
else:
    print('You got {} wrong.  Keep trying!\n'.format(num_wrong))
print(output_frame.to_string(index=False))

Membangun (Multi-layer) Perceptron XOR dari Perceptron AND, OR, dan NOT #

Operator logika XOR, akan menghasilkan 1 (True) jika salah satu input bernilai 1 (eksklusif), selain itu akan menghasilkan 0 (False).

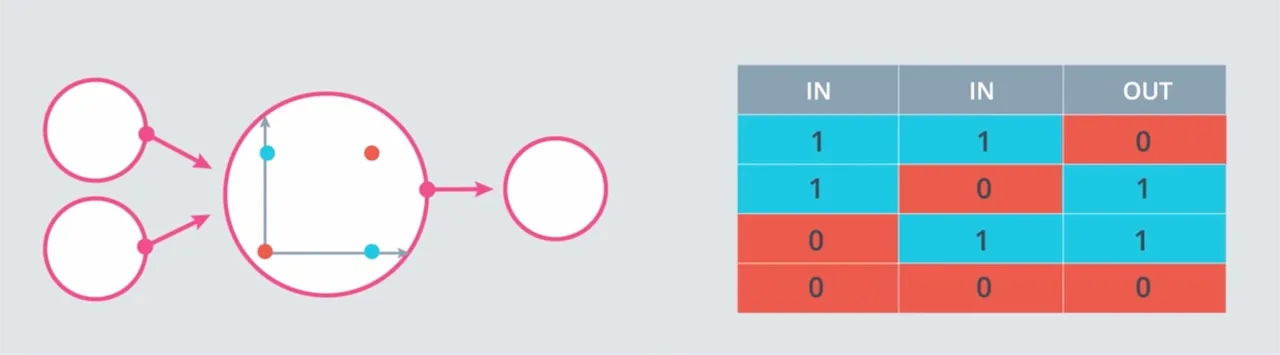
Sebetulnya operator logika XOR ini dapat dibangun dari sejumlah operator AND, OR, dan NOT. Salah satu referensinya di wiki XOR ^{1 2}.

Mengutip dari stackoverflow ³:

So, XOR is just like OR, except it’s false if A and B are true.

So, (A OR B) AND (NOT (A AND B)), which is (A OR B) AND (A NAND B)

Multi-layer Perceptron XOR #

Bisa digunakan untuk menjawab pertanyaan tentang multi-layer perceptron yang pertama dibuat:

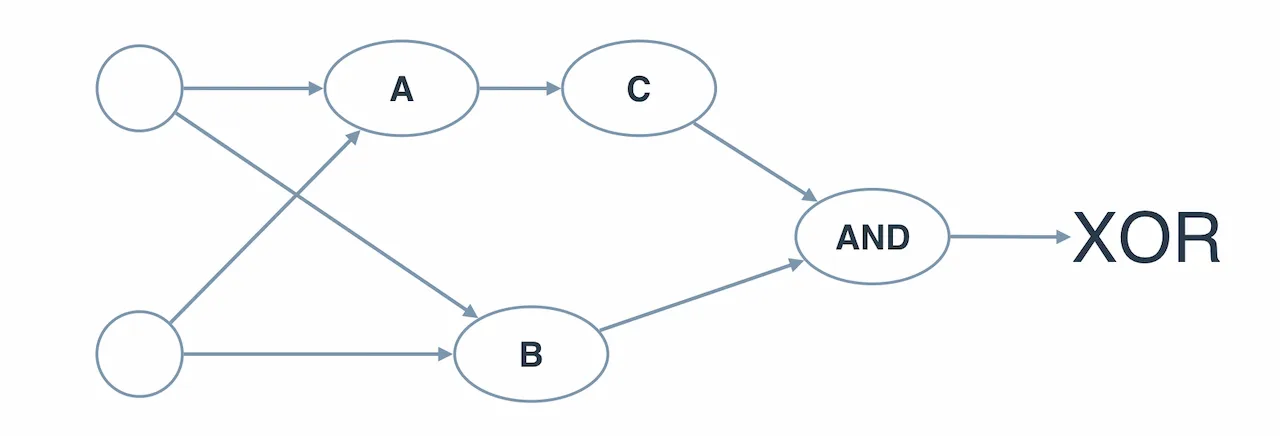
Trik dari Perceptron #

Di bagian sebelumnya kita membuat perceptron XOR dengan menggunakan perceptron AND, OR, dan NOT.

Tapi pada kenyataannya, di kondisi lapangan, kita nggak bisa membangun perceptron ini sendiri. Idenya adalah memberikan perceptron itu nilai hasil yang diinginkan, kemudian perceptron itu membangun dirinya sendiri.

Ada trik yang dapat digunakan untuk mencapai tujuan tersebut.. 🙌

Kita kembali pada contoh kondisi klasifikasi diterima di kampus, dengan pertanyaan: bagaimana mencari persamaan yang paling sesuai untuk garis yang memisahkan dua kelompok data tersebut?

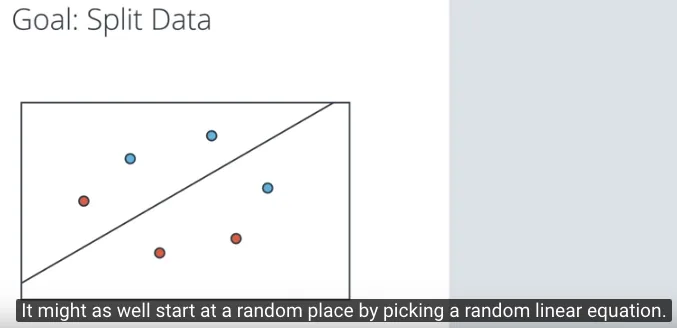
Dengan tujuan untuk memisahkan dua kelompok data, kita akan menyederhanakan kondisinya, dengan hanya 3 titik biru dan 3 titik merah. Kemudian memulai memisahkan dengan random di awalnya untuk menghasilkan sebuah garis acak yang akan mencoba memisahkan kelompok biru dan merah.

Hasilnya ada 4 titik sudah sesuai dengan pengelompokannya dan 2 titik yang masih belum sesuai. Kita akan fokus pada dua titik ini, dimana 1 titik merah masih berada di area biru dan 1 titik biru masih berada di area merah.

Di titik yang masih salah klasifikasi, triknya adalah menggeser garis pemisah ini mendekati (hingga sedikit melewati) titik tersebut, sehingga titik tersebut berpindah klasifikasi ke area yang seharusnya.

Secara matematika, bagaimana menggeser sebuah garis mendekati suatu titik?

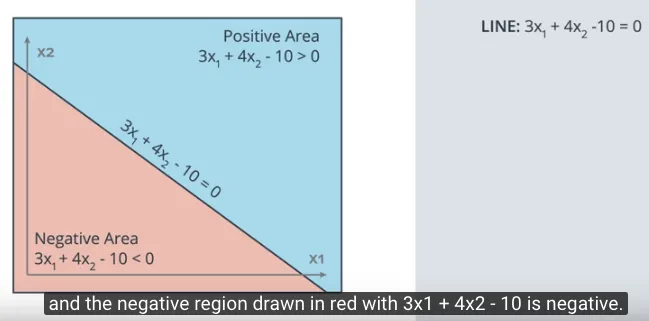
Misalnya ada sebuah garis pemisah dengan persamaan: $3x_1 + 4x_2 -10 = 0$ dalam gambar berikut memisahkan area merah dimana persamaannya bernilai negatif (<0) dan area biru dimana persamaannya bernilai positif (>0).

Kemudian ada satu titik, misalnya titik merah (4, 5) salah klasifikasi berada di area biru (area positif).

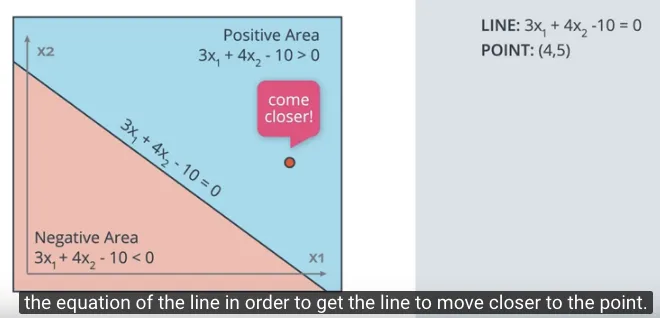
Implementasi secara matematika, kita gunakan parameter dari persamaan $3x_1 + 4x_2 -10 = 0$ yaitu 3, 4, dan -10. Kemudian parameter dari titik (4, 5) yaitu 4, 5, dan 1 (angka 1 ini ditambahkan sebagai unit bias).

Untuk menggeser garis dengan persamaan tersebut ke titik, karena titik ini berada di area positif maka kedua parameternya dikurangkan.

 3     4     -10
 4     5      1
________________ - (dikurangi)
-1    -1     -11

Hasil pengurangan tersebut, adalah persamaan garis yang baru yaitu $-x_1 - x_2 -11 = 0$. Jika digambarkan, garis ini akan langsung bergeser secara drastis mendekati titik (4, 5) dan membuat titik tersebut berada di area yang benar. Sedangkan kita tidak mau perubahan drastis tersebut membuat sejumlah titik lain yang sebelumnya sudah berada di area yang benar menjadi berubah di area yang salah. Kita ingin melakukan perubahan dengan sedikit demi sedikit (small steps) mengarah ke titik tersebut. Di sinilah kita membutuhkan learning rate.

Learning Rate #

Learning Rate adalah sebuah angka kecil misalnya 0.1 atau 0.01 yang akan digunakan untuk memroses perubahan sedikit demi sedikit (small steps) dalam hal penyesuaian persamaan linear.

Jika learning rate ini digunakan, maka kita akan mengalikan learning rate 0.1 ini ke parameter dari titik (4, 5), sehingga menghasilkan: 0.4, 0.5, 0.1 (angka yang terakhir dari unit bias). Kembali dilakukan operasi pengurangan, karena titik tersebut salah di area positif.

 3     4     -10
0.4   0.5    0.1
_________________ - (dikurangi)
2.6   3.5   -10.1

Sehingga persamaan garis yang baru adalah $2.6x_1 + 3.5_2 -10.1 = 0$. Dan garis ini mulai mendekat ke arah titik (4, 5), sesuai yang diharapkan.

Untuk melengkapi contoh, kemudian ada satu titik lagi, misalnya titik biru (1, 1) salah klasifikasi berada di area merah (area negatif).

Karena titik (1, 1) salah klasifikasi di area merah (area negatif), maka kita akan melakukan operasi penambahan. Dengan mengalikan learning rate 0.1 ini ke parameter dari titik (1, 1) menghasilkan 0.1, 0.1, 0.1 (angka yang terakhir dari unit bias).

 3     4     -10
0.1   0.1    0.1
_________________ + (ditambahkan)
3.1   4.1   -9.9

Sehingga persamaan garis yang baru adalah $3.1x_1 + 4.1x_2 -9.9 = 0$. Dan garis ini mulai mendekat ke arah titik (1, 1), sesuai yang diharapkan.

Misalnya kita menggunakan learning rate bernilai 0.01 artinya akan membutuhkan 100 steps untuk membuat persamaan garis tersebut menjadi benar dalam klasifikasi titik, misalnya (1, 1) di area biru (area positif).

Algoritma untuk Perceptron #

Pseudocode yang akan digunakan dalam pembuatan perceptron menggunakan trik di atas adalah:

1. Start with random weights: $w_1, …, w_n, b$

2. For every misclassified point $(x_1, …, x_n)$:

   2.1. If prediction = 0:

   • For i = 1 … n
     • Change $w_i + \alpha x_i$
   • Change $b$ to $b + \alpha$

   2.2. If prediction = 1:

   • For i = 1 … n
     • Change $w_i - \alpha x_i$
   • Change $b$ to $b - \alpha$

Dengan catatan:

• prediction = 0 artinya seharusnya positif tapi salah klasifikasi di area negatif, sehingga digeser dengan menambahkan $\alpha$.
• prediction = 1 artinya seharusnya negatif tapi salah klasifikasi di area positif, sehingga digeser dengan mengurangkan $\alpha$.
• $\alpha$ adalah learning rate

Membuat Kode (coding) untuk Algoritma Perceptron #

Karena pembahasannya panjang, hanya terkait untuk kode ini, maka dibuatkan halaman khusus Membuat Kode Algoritma Perceptron, karena ada jawaban dari quiz sehingga pertimbangkan dalam membuka halaman tsb.

Algoritma Perceptron yang Non-Linear #

Setelah sebelumnya membahas perceptron yang memisahkan dua kelompok data dengan sebuah garis (persamaan linear), ke depan akan lebih kompleks dengan pemisahan dua kelompok data dengan persamaan yang tidak lagi linear, misalnya kuadratik, atau persamaan lingkaran, dls.

Sebelum mulai membahas ke persamaan yang lebih kompleks, kita akan membahas beberapa hal pendukungnya terlebih dahulu.

Fungsi Error #

Fungsi error adalah sebuah fungsi yang akan menginformasikan sejauh apa nilai (kesalahan, error) dari prediksi yang kita lakukan, biasanya dibanding dengan label atau data latih. Di kelas Udacity, fungsi error (error function) didefinisikan sebagai sebuah fungsi yang memberikan informasi sejauh apa kita dari solusi.

Fungsi error ini selanjutnya akan membantu kita dalam proses mencari solusi dari permasalahan (implementasi Neural Networks).

Fungsi error tidak boleh bernilai bilangan bulat (discrete), tetapi harus bernilai pecahan (continuous). Dengan langkah (steps) yang kecil, maka akan sulit mencari apakah fungsi error sudah mulai mengecil atau belum. Misalnya:

untuk langkah kecil 0.2, maka nilai 1 ditambah/dikurangi 0.2, dalam bilangan bulat, masih bernilai 1.

Fungsi error harus bisa diturunkan secara matematika (differentiable), akan dibahas lebih lanjut nanti.

Lalu bagaimana gagasan fungsi error ini bisa digunakan untuk memecahkan masalah sebelumnya, mencari sebuah garis yang dapat memisahkan dua kelompok data?

Caranya dilakukan dalam dua langkah:

1. Memberikan nilai penalty dari setiap titik, dimana nilai penalty akan besar apabila titik (salah klasifikasi sehingga) berada area yang salah, serta nilai penalty bernilai kecil (hampir mendekati 0) apabila titik sudah sesuai (klasifikasi) berada di areanya.
2. Menjumlahkan nilai penalty dari semua titik, kemudian mencari persamaan garis (misalnya dengan menggeser-gesernya), hingga dapat mengurangi total nilai error (hasil penjumlahan nilai penalty). Tampak pada gambar berikut bahwa ada 2 titik yang ukurannya besar, menggambarkan bahwa kedua titik tersebut masih salah dalam klasifikasi.

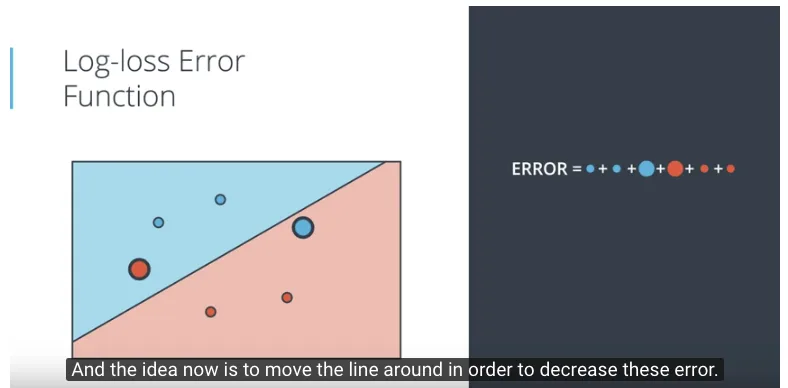
Dengan menggeser-geserkan garis untuk memisahkan dua kelompok data, dengan cara mencari total nilai error yang paling kecil, akhirnya didapatkan gambaran sebagai berikut.

Selanjutnya, bagaimana mendefinisikan fungsi error ini, kemudian bagaimana penggunaannya dalam metode gradient descent? akan dijelaskan berikutnya.

Fungsi Sigmoid untuk Fungsi Aktivasi #

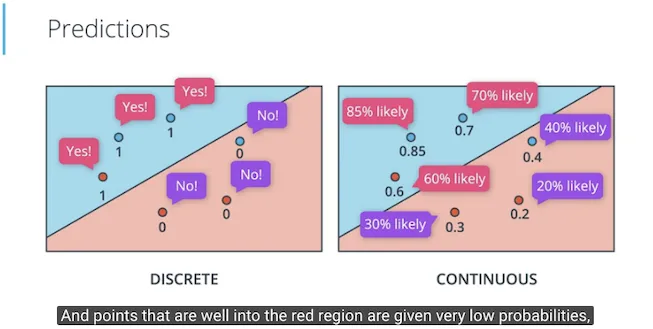
Jika fungsi error dipilih untuk menggunakan nilai pecahan (continuous), maka demikian juga dengan nilai prediksi dapat dipilih untuk menggunakan nilai pecahan (continuous) juga. Di prediksi discrete kita menggunakan label ya atau tidak, diterima atau ditolak, dls. Di prediksi continuous, kita menggunakan prosentase kemungkinan (probabilty), misalnya 80% kemungkinan diterima, dls.

Dalam contoh di atas, sebelumnya prediksi antara diterima di kampus atau ditolak, diubah menjadi prediksi continues berarti menjadi berapa prosentase kemungkinan diterima. Dalam gambar berikut jika biru adalah diterima maka titik biru 0.85 artinya 85% kemungkinan diterima, sedangkan titik merah 0.2 artinya 20% kemungkinan diterima.

Pengubahan prediksi yang sebelumnya discrete menggunakan step function, menjadi prediksi continuos menggunakan sigmoid function sebagai fungsi aktivasi (activation function). Fungsi sigmoid ini akan mengubah nilai masukan positif yang besar menghasilkan nilai mendekati 1, nilai masukan negatif yang besar menghasilkan nilai mendekati 0, dan nilai masukan mendekati 0 akan menghasilkan nilai mendekati 0.5.

Persamaan dari fungsi sigmoid ini adalah:

| $\sigma(x) = \frac{1}{1 + e^-x}$

Berikut adalah gambaran saat persamaan $Wx + b$ dimasukkan pada fungsi sigmoid.

• Saat nilai dari $Wx + b$ positif yang besar, keluaran dari fungsi sigmoid adalah mendekati 1
• Saat nilai dari $Wx + b$ negatif yang besar, keluaran dari fungsi sigmoid adalah mendekati 0
• Dan di garis utamanya, dimana $Wx + b$ bernilai 0, keluaran dari fungsi sigmoid adalah 0.5

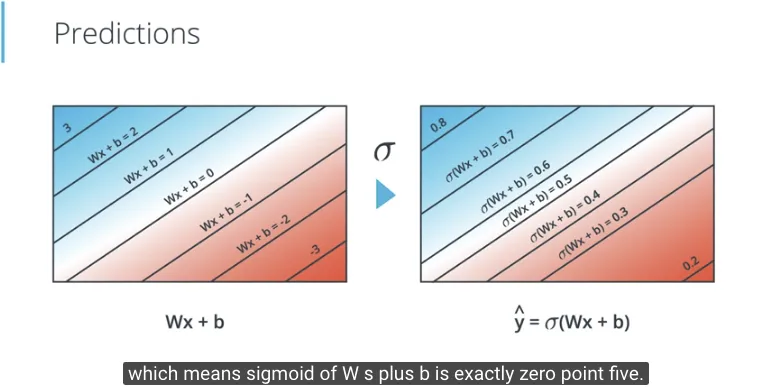
Setelah memahami fungsi sigmoid sebagai fungsi aktivasi (activation function), saatnya menerapkannya ke Perceptron, sehingga keluarannya berada pada nilai continues antara 0 dengan 1.

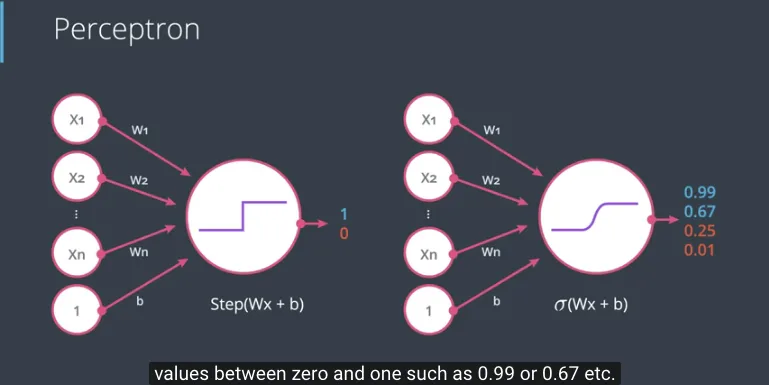
Klasifikasi Multi-class #

Jika sebelumnya jika hanya membahas klasifikasi dua class (binary classification), misalnya diterima atau ditolak masuk kampus. Berikut akan kita bahas klasifikasi lebih dari dua class, misalnya menentukan apakah binatang bebek (duck), berang-berang (beaver), atau anjing laut (walrus).

Fungsi Softmax #

Untuk dapat melakukan prediksi dengan nilai continues seperti halnya fungsi Sigmoid, untuk klasifikasi 3 class atau lebih, menggunakan fungsi Softmax. Probability dari class $i$, dengan score dari fungsi linear bernilai $z_1, …, z_n$.

$P(i) = \frac{e^{z_i}}{e^{z_1} + … + e^{z_n}}$

Fungsi eksponential atau $e$ adalah sebuah fungsi yang selalu memberikan nilai positif untuk semua masukan, baik itu masukannya positif ataupun negatif, besar ataupun kecil.

Pseudocode fungsi Softmax menggunakan NumPy (import numpy as np):

• np.exp() seperti yang sudah diprediksi ini adalah fungsi untuk exponential, tapi fungsi ini menerima input bukan hanya skalar, bahkan juga bisa sebuah NumPy array. Jadi fungsi exponential-nya di-broadcast ke seluruh element array, masing-masing dilakukan operasi exponential. Di bawah ini fungsi np.array() akan membentuk NumPy array dari sebuah List Python.

  print(np.exp(np.array([2, 1, 0])))  # [7.3890561  2.71828183 1.        ]
  

• np.sum juga sesuai dengan namanya akan melakukan summation atau penambahan, termasuk fungsi yang menerima input berupa NumPy array, jadi seluruh elemennya akan dijumlahkan. Sebagai contoh, jika NumPy array hasil yang dicetak di atas dijumlahkan, hasilnya adalah:

  print(np.sum(np.exp(np.array([2, 1, 0]))))  # 11.107337927389695
  

• Untuk membagi, kita bisa menggunakan operator pembagi biasa ( /), atau menggunakan fungsi np.divide(), yang bisa melakukan operasi broadcast untuk membagi suatu NumPy array dengan suatu skalar, jadi seluruh elemennya akan dibagi dengan skalar tersebut.

Tinggal menggabungkan tiga fungsi tersebut, untuk membuat fungsi Softmax menggunakan NumPy.

Yang seru, pertanyaan di salah satu materi video, apakah Softmax untuk n = 2 bernilai sama dengan Sigmoid? Untuk kasus khusus dimana n = 2, fungsi Softmax sama dengan fungsi Sigmoid (atau di beberapa referensi disebut fungsi Logistic). Salah satu yang menjelaskan penurunan rumusnya di situs deeplearning stanford ⁴, di situ diberikan sebutan bahwa Softmax regression itu adalah multinomial Logistic regression, sehingga dalam kasus binary akan sama dengan Logistic regression atau Sigmoid. Nanti akan dibahas selanjutnya mengenai Logistic regression.

One-Hot Encoding #

Pada contoh kasus yang digunakan sebelumnya, datanya tersedia dalam bentuk angka, misalnya hasil ujian. Tapi kadang data masukan yang dimiliki tidak berbentuk angka, misalnya berbentuk kategori, untuk itu digunakan proses One-Hot Encoding yang akan mendefinisikan setiap jenis kategori sebagai satu kolom data, kemudian nilainya hanya 1 atau 0 sesuai dengan kategorinya.

Pada gambar di atas, adalah One-Hot Encoding untuk 3 class: duck, beaver, walrus. Salah satu yang penting di sini adalah tidak ada ketergantungan antara masing-masing class, sehingga tidak menggunakan nilai urut, misalnya duck 0, beaver 1, walrus 2.

Maximum Likelihood #

Masih membahas seputar pemilihan model yang memisahkan dua kelompok data sebelumnya. Mana model yang paling baik dalam memisahkan dua kelompok data?

Dalam membahas tentang statistik, probabilitas misalnya dari dua buah model, mana yang lebih akurat? Model yang terbaik adalah model yang memberikan probabilitas paling besar untuk seluruh label (data latih) yang ada di kedua kelompok tersebut. Hal ini disebut dengan maximum likelihood.

Metode maximum likelihood dengan memilih model yang memberikan nilai probabilitas tertinggi untuk label yang ada. Demikian sehingga memaksimalkan probabilitas, kita bisa memilih model terbaik.

Kembali membahas prediksi dari setiap titik dari kedua kelompok adalah $\hat{y} = \sigma(Wx + b)$ sehingga probabilitas dari sebuah titik adalah biru (blue) ditentukan dengan:

$P(blue) = \sigma(Wx + b)$

Sehingga probabilitas dari seluruh data dari kedua kelompok adalah dot product dari setiap probabilitas titik yang ada, atau dengan kata lain, perkalian dari semua probabilitas titik yang ada.

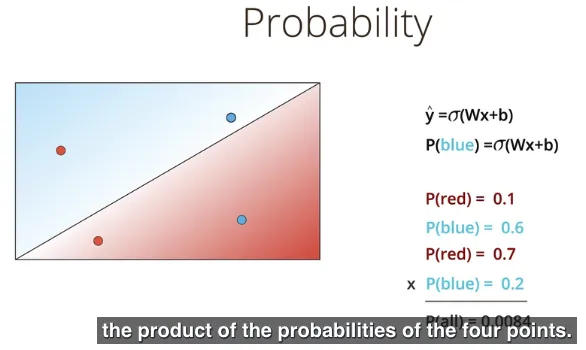
Apakah memaksimalkan probabilitas dari suatu model sama artinya dengan meminimalkan fungsi error? Kita akan lihat dalam pembahasan berikut.

Kembali membahas sebelumnya yang menghitung probabilitas dari seluruh data dengan melakukan perkalian (product) dari setiap probabilitas titik. Sayangnya perkalian (misalnya untuk ribuan data) adalah proses yang membutuhkan sumber daya (resource) besar dimana keseluruhan datanya adalah pecahan (antara 0 dan 1), hasilnya akan pecahan yang sangat kecil, untuk itu dibutuhkan operator lain yang lebih hemat sumber daya.

Fungsi $log$ akan mengubah perkalian (products) menjadi penjumlahan (sum). Berikut adalah sifat dari logaritma (basis bilangan 10) yang digunakan:

$log(A * B) = log(A) + log(B)$

Dengan menggunakan basis bilangan $e$, operator logartima yang digunakan adalah logaritma natural $ln()$.

$ln(A * B) = ln(A) + ln(B)$

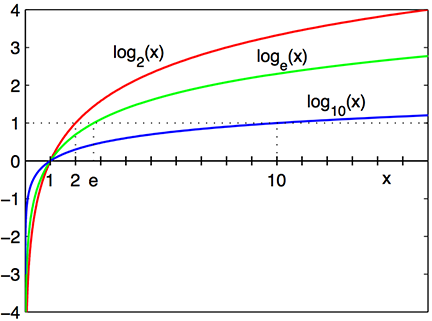
Plot Logaritma tersebut dari artikel wiki ⁵. Perhatikan bahwa untuk nilai pecahan antara 0 dan 1, hasil dari logaritmanya adalah negatif.

Cross Entropy #

Cross Entropy adalah sebuah konsep yang menjumlahkan nilai negatif dari logaritma propabilitas untuk setiap data.

Model yang baik akan memiliki nilai cross entropy yang kecil, sedangkan model yang buruk akan memiliki nilai cross entropy yang besar. Sebetulnya ini terkait dengan perhitungan probabilitas sebelumnya, model yang baik akan memiliki probabilitas yang besar, dimana hasil operasi negatif dari logaritma nilai yang besar (cross entropy) adalah nilai yang kecil.

Bahkan cross entropy ini bisa diberlakukan untuk setiap titik, jadi bukan hanya penjumlahannya saja. Terlihat pada gambar berikut ini bahwa suatu titik yang salah dikasifikasikan (misclassified), akan memiliki nilai cross entropy yang besar. Hal ini mengingatkan kembali pada fungsi error, dimana suatu titik yang salah diklasifikasikan akan memiliki nilai error yang besar, sebaliknya titik yang diklasifikasikan dengan benar akan memiliki nilai error yang kecil.

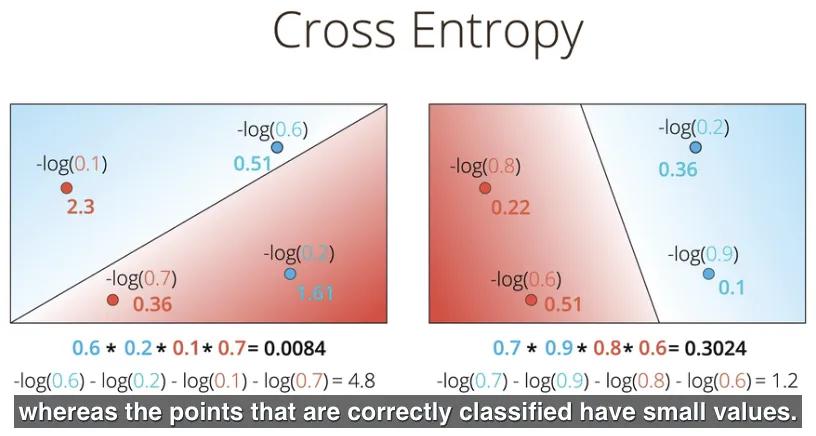
Kembali membahas mengenai mencari model yang terbaik, sehingga saat ini tujuan (caranya) sudah berubah, dari memaksimalnya probabilitas, menjadi meminimalkan nilai cross entropy. Sebagai hasil keterhubungan antara probabilitas dan fungsi error.

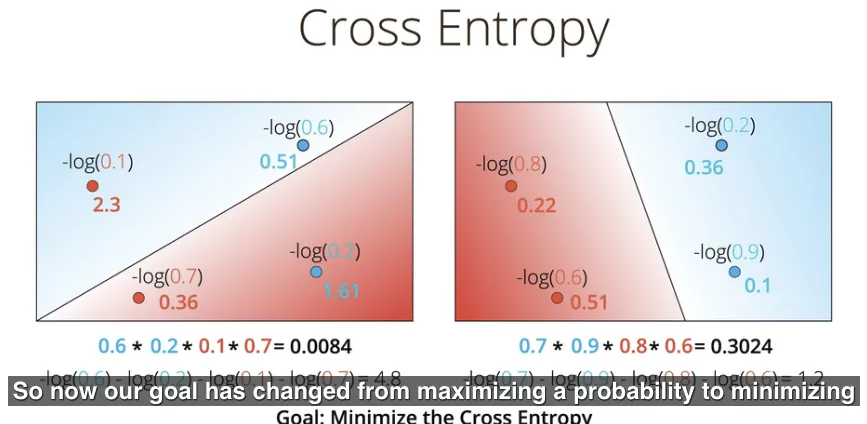
Konsep cross entropy ini sangat popular di berbagai bidang, salah satunya Machine Learning. Formulanya adalah

Cross-Entropy = $-\sum_{i=1}^m y_iln(p_i) + (1 - y_i)ln(1 - p_i)$

Untuk dalam kasus di gambar berikut adalah:

• $i$ akan bernilai 1 sampai $m$ yaitu 3 (jumlah banyaknya event dalam hal ini jumlah pintu)
• $p_1$ adalah probabilitas untuk ada hadiah di pintu ke-1, sebaliknya $(1 - p_1)$ adalah probabilitas untuk tidak ada hadiah di pintu ke-1. begitu juga untuk $p_2$ dan $(1 - p_2)$ serta $p_3$ dan $(1 - p_3)$.
• $y_1$ akan bernilai 1 jika ada hadiah di pintu ke-1 atau bernilai 0 tidak tidak ada hadiah di pintu ke-1. begitu juga untuk $y_2$ serta $y_3$.

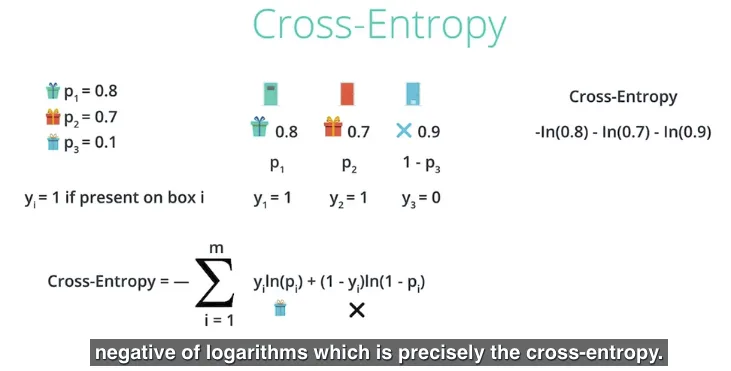
Sebagai contoh, melakukan kalkulasi cross-entropy untuk pasangan:

• cross_entropy((1, 1, 0), (0.8, 0.7, 0.1)) menghasilkan 0.69.

  di sini (1, 1, 0) adalah nilai dari ($y_1$, $y_2$, $y_3$).

  di sini (0.8, 0.7, 0.1) adalah nilai dari ($p_1$, $p_2$, $p_3$).

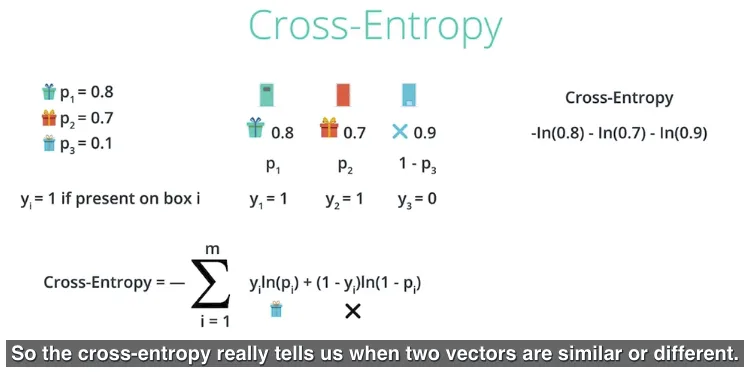
  menghasilkan nilai cross-entropy yang kecil, karena (1, 1, 0) itu mirip (similar) dengan vector (0.8, 0.7, 0.1).

  artinya pengaturan hadiah dengan kumpulan nilai (1, 1, 0) kemungkinan besar terjadi berdasarkan nilai propabilitas dengan kumpulan nilai (0.8, 0.7, 0.1).

• cross_entropy((0, 0, 1), (0.8, 0.7, 0.1)) menghasilkan 5.12.

  di sini (0, 0, 1) adalah nilai dari ($y_1$, $y_2$, $y_3$)). di sini (0.8, 0.7, 0.1) adalah nilai dari ($p_1$, $p_2$, $p_3$).

  menghasilkan nilai cross-entropy yang besar, karena (0, 0, 1) itu tidak mirip dengan vector (0.8, 0.7, 0.1).

  artinya pengaturan hadiah dengan kumpulan nilai (1, 1, 0) kemungkinan besar tidak terjadi berdasarkan nilai probabilitas dengan kumpulan nilai (0.8, 0.7, 0.1).

Seperti apa kode dari formula cross_entropy(Y, P) dimana Y adalah List kategori dan P adalah List probabilitas?

ternyata di quiz ini udacity menggunakan salah satu contoh dengan data berikut; Y bernilai [1, 0, 1, 1] dan P bernilai [0.4, 0.6, 0.1, 0.5].

• kita bisa menggunakan fungsi zip() untuk sekaligus mengiterasi Y dan P. Atau, pilihan yang lain, kita menggunakan kemampuan broadcast dari NumPy sehingga tidak perlu melakukan iterasi secara manual, dengan catatan bahwa kita perlu konversi List menjadi NumPy array, misalnya dengan fungsi np.array(Y) atau jika kita mau konversi semua isinya menjadi NumPy array bertipe float, kita gunakan np.float_(P).
• lalu kita hitung perkalian $y_1 * log(p_1)$ sebagai _y * np.log(_p), dengan fungsi logaritma dari NumPy. di NumPy np.log itu menggunakan basis $e$ sedangkan basis 10 adalah np.log10. jangan lupa bahwa np.log itu bisa melakukan operasi broadcast sehingga perkalian dengan setiap elemen tidak perlu iterasi.
• lalu kita hitung perkalian $(1-y_1) * log(1-p_1)$ sebagai (1-_y) * np.log(1-_p)
• tambahkan semuanya, untuk penggunaan broadcast bisa menggunakan fungsi np.sum dari NumPy, terakhir jangan lupa kalikan dengan -1.0 untuk mendapatkan cross-entropy

Jika berhasil, artinya kita sudah membuat kode cross-entropy untuk 4 events (kemungkinan hadiah akan muncul di pintu), yaitu pada contoh sebelumnya artinya untuk 4 pintu. 🙌

Multi-class Cross-Entropy #

Jika sebelumnya hanya membahas klasifikasi 2 (binary) tentang ada atau tidaknya hadiah di balik pintu, lalu bagaimana kalo mencoba melakukan klasifikasi 3 (atau lebih), misalnya menebak binatang apa di balik pintu, apakah bebek (duck), berang-berang (beaver), atau anjing laut (walrus)?

Sebagai contoh gambar berikut berisi probabilitas dari bebek berada di pintu ke-1 adalah 0.7, berang-berang berada di pintu ke-1 adalah 0.2, anjing laut berada di pintu ke-1 adalah 0.1, dan selanjutnya untuk pintu ke-2 serta ke-3. Jika diperhatikan total dari probabilitas di setiap pintu (kolom) adalah 1, artinya ada sudah pasti 1 satu binatang di balik pintu, hanya saja kemungkinannya berbeda-beda, dan juga artinya ada kemungkinan lebih dari satu pintu akan muncul binatang yang sama, misalnya anjing laut di pintu 2 dan juga anjing laut di pintu 3.

Perhitungan cross-entropy-nya akan sama dengan sebelumnya, penjumlahan negatif logaritma dari probabilitas event.

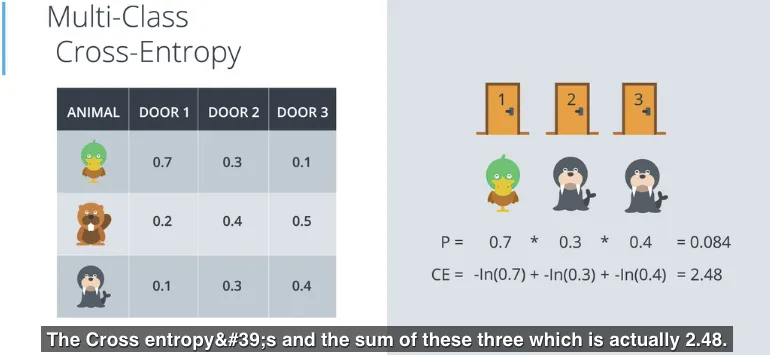
Berikut adalah formula dari Multi-class Cross-Entropy:

Multi-class Cross-Entropy = $-\sum_{i=1}^m \sum_{j=1}^n y_{ij} ln(p_{ij})$

dengan catatan, ini $\sum_{i=1}^m$ dengan $\sum_{j=1}^n$ dibalik posisinya dibandingkan dengan yang ada di gambar di bawah (di video kelas):

• $m$ adalah jumlah (multi) class, dalam hal ini m = 3 (duck, beaver, walrus). Dalam formula di atas, variable $i$ akan iterasi dari 1 sampai $m$.
• $n$ adalah jumlah pintu, dalam hal ini n = 3. Dalam formula di atas, variabel $j$ akan iterasi dari 1 sampai $n$. Terlihat dalam gambar di bawah, $j$ tertulis di pintu.
• $p_{ij}$ adalah probabilitas untuk event (kemunculan) dari class $i$ di pintu $j$.
• $y_{ij}$ akan bernilai 1 jika muncul class $i$ di pintu $j$, sebaliknya akan bernilai 0.

Seperti sebelumnya, muncul pertanyaan, jika formula Multi-class Cross-Entropy ini diberikan nilai class = 2, apakah sama formulanya dengan Cross-Entropy? Jawabnya sama. (masih butuh referensi tambahan untuk penurunan formulanya 🤔 ).

Algoritma Logistic Regression #

Pada dasarnya langkah yang dilakukan seperti ini:

• ambil data
• pilih model secara acak
• hitung error
• minimalkan nilai error, dan dapatkan model yang lebih baik
• enjoy!

berikutnya akan dijelaskan beberapa langkah yang terkait.

Menghitung fungsi Error #

Di sini Error pada satu point dengan prediksi untuk klasifikasi binary adalah

Error = $- (1 - y)(ln(1 - \hat{y})) - yln(\hat{y})$

dimana $y$ adalah label bernilai $1$ jika blue (salah satu klasifikasi), atau bernilai $0$ jika red (klasifikasi lainnya). probabilitas dari blue atau $P(blue)$ adalah $\hat{y}$, artinya probabilitas dari red adalah $(1 - \hat{y})$, karena probabilitas dari red adalah 1 - probabilitas dari blue untuk kondisi klasifikasi binary.

Fungsi Error untuk klasifikasi binary (2 class) adalah

Error Function = $-\frac{1}{m} \sum_{i=1}^m y_{i} ln(\hat{y_{i}}) + (1 - y_i) ln(1 - \hat{y_{i}})$

dimana prediksi $\hat{y_i} = \sigma(Wx^{(i)} + b)$, fungsi Sigmoid dari fungsi linear $Wx + b$, dengan $y_i$ adalah label dari point $x^{(i)}$, artinya

E(W, b) = $-\frac{1}{m} \sum_{i=1}^m y_{i} ln(\sigma(Wx^{(i)}+b)) + (1 - y_i) ln(1 - \sigma(Wx^{(i)}+b))$

Fungsi Error untuk klasifikasi multi-class (3 class atau lebih) adalah

error = $-\frac{1}{m} \sum_{i=1}^m \sum_{j=1}^n y_{ij} ln(\hat{y_{ij}})$

Meminimalkan fungsi Error #

Dengan fungsi Error seperti dituliskan di atas E(W, b) dimana fungsi Error sebagai fungsi dari weights kemudian tujuan kita adalah meminimalkan fungsi Error ini.

Kita mulai di awal dengan memberikan nilai weights secara acak E(W,b), dimana menghasilkan prediksi dengan fungsi Sigmoid, $\sigma(x) = Wx + b$. Dengan fungsi Error yang didefinisikan

E(W, b) = $-\frac{1}{m} \sum_{i=1}^m y_{i} ln(\sigma(Wx^{(i)}+b)) + (1 - y_i) ln(1 - \sigma(Wx^{(i)}+b))$

Fungsi Error tersebut merupakan penjumlahan dari Error untuk setiap point, dimana menghasilkan nilai Error yang besar apabila salah klasifikasi (misclassified), sebaliknya nilai Error yang kecil apabila dikasifikasikan dengan benar.

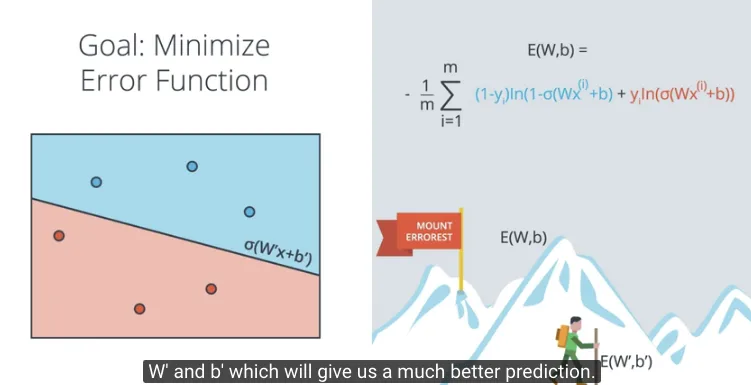
Proses meminimalkan fungsi Error dengan menggunakan Gradient Descent (yang akan dibahas berikutnya), hingga dengan nilai weights baru E(W’,b’) menghasilkan fungsi Error yang nilainya minimal, berdasarkan prediksi dengan fungsi Sigmoid, $\sigma(x) = W’x + b’$.

Perhitungan Gradient #

Untuk mencari nilai minimal fungsi error, kita perlu membuat turunan (derivative) dari fungsi error. Ini sama dengan pelajaran matematika (kalkulus) tentang gradien.

Kita bahas dahulu turunan dari fungsi Sigmoid, berikut adalah fungsi Sigmoid:

$\sigma(x) = \frac{1}{1+e^{-x}}$

Turunan dari fungsi Sigmoid terhadap $x$ adalah ($\frac{\partial}{\partial(x)}$ adalah notasi partial derivative)

$\sigma’(x) = \frac{\partial}{\partial(x)} \frac{1}{1+e^{-x}}$

$ = \frac{e^{-x}}{(1+e^{-x})^2}$

$ = \frac{1}{1+e^{-x}} \frac{e^{-x}}{1+e^{-x}}$

$ = \frac{1}{1+e^{-x}} (\frac{1+e^{-x}}{1+e^{-x}} - \frac{1}{1+e^{-x}})$

$\sigma’(x) = \sigma{(x)} (1 - \sigma(x))$

Algoritma Gradient Descent #

Kembali membahas fungsi Error. Jika punya $m$ points yang dengan label $y_1$, $y_2$, …, $y_m$, maka fungsi Error nya adalah

$E = -\frac{1}{m} \sum_{i=1}^m (y_{i} ln(\hat{y_{i}}) + (1 - y_i) ln(1 - \hat{y_{i}}))$

Dimana prediksi $\hat{y} = \sigma(Wx^{(i)} + b)$

Tujuan kita adalah menghitung gradien dari $E$, di titik $x = (x_1, …, x_n)$, dihasilkan dari parsial derivative

$\nabla{E} = (\frac{\partial}{\partial{w_1}}E, …, \frac{\partial}{\partial{w_n}}E, \frac{\partial}{\partial{b}}E)$

TODO

$\frac{\partial}{\partial{w_j}}\hat{y} = \hat{y}(1-\hat{y}).x_j$

TODO

$\frac{\partial}{\partial{w_j}}E = -(y - \hat{y}).x_j$

Dengan perhitungan yang mirip, kita bisa mendapatkan

$\frac{\partial}{\partial{b}}E = -(y - \hat{y})$

Kesimpulannya, gradien sebagai berikut

$\nabla{E} = -(y - \hat{y})(x_1, …, x_n, 1)$

Gradien sebetulnya adalah sebuah skalar kali koordinat dari point.

Di sini skalar adalah sejumlah perbedaan antara label dan prediksi.

ini sama dengan Algoritma Perceptron

Gradient Descent Step #

Dengan gradient descent step sesederhana mengurangkan sejumlah gradien dari fungsi Error untuk semua titik, maka pembaruan weights menggunakan langkah berikut:

$w’_i \leftarrow w_i - \alpha [ -(y - \hat{y}) x_i ]$

yang mana ekivalen dengan

$w’_i \leftarrow w_i + \alpha (y - \hat{y} x_i)$

Langkah yang sama untuk pembaruan bias berikut:

$b’ \leftarrow b + \alpha (y - \hat{y})$

Catatan: Dengan mengambil nilai rata-rata dari Error, istilah yang digunakan seharusnya $\frac{1}{m}.\alpha$ daripada $\alpha$, tapi karena $\alpha$ adalah konstanta, untuk menyederhanakan kalkulasi, kita akan menggunakan $\frac{1}{m}.\alpha$ sebagai learning rate dalam perhitungan, tapi penulisan notasi dibiarkan tetap memanggilnya $\alpha$.

Algoritma Logistic Regression #

Berikut adalah pseudo-code untuk Algoritma Logistic Regression

1. Dimulai dengan memilih weights secara acak: $w_1, …, w_n, b$

2. Untuk semua titik dengan koordinat $(x_1, …, x_n)$:

   2.1. Untuk i=1 ... n:

   .. 2.1.1. Perbarui $w’_i \leftarrow w_i - \alpha \frac{\partial{E}}{\partial{w_i}}$ dimana $\frac{\partial{E}}{\partial{w_i}} = (\hat{y}-y)x_i$

   .. 2.1.2. Perbarui $b’ \leftarrow b - \alpha \frac{\partial{E}}{\partial{b}}$ dimana $\frac{\partial{E}}{\partial{b}} = (\hat{y}-y)$

3. Ulangi hingga Error jadi kecil, atau ulangi sejumlah kali, jumlah ini biasa disebut epochs.

Jika dilihat, ini sama dengan Algoritma Perceptron

TBD